Como Funciona a Função Quartil no Excel?

Sumário

Conceitos Básicos
Funções Disponíveis no Excel
Função QUARTIL.INC
Função QUARTIL.EXC
Considerações Finais
Leituras Recomendadas
Download de Arquivos

Se preferir, você pode assistir em vídeo às explicações dadas neste artigo.

Conceitos Básicos

Uma das formas de analisar grandes conjuntos de dados é por meio do cálculo de estatísticas descritivas. Isso inclui indicadores como a média, mediana, desvio padrão, mínimo, máximo, quartis 1 e 3, amplitude interquartil, etc. Para facilitar esse tipo de análise, muitas pessoas recorrem ao Excel, que oferece fórmulas muito fáceis de usar e interpretar.

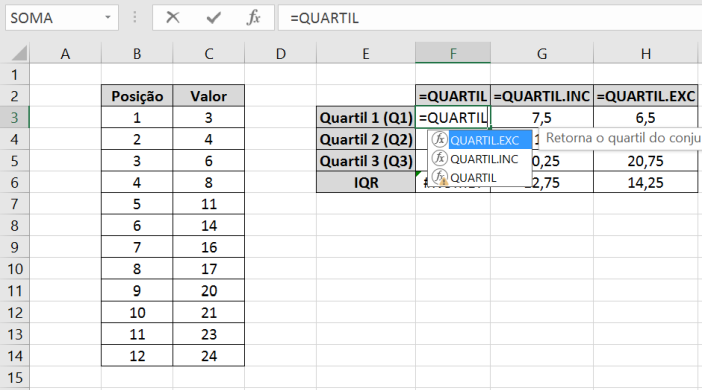
Entretanto, isso deixa de ser verdade no caso do cálculo dos quartis. Até a versão 2007, o Excel só possuía uma função para o cálculo de quartis (“=QUARTIL”). A partir da versão 2010, o Excel passou a contar com 2 novas funções (“=QUARTIL.INC” e “=QUARTIL.EXC”) para calcular quartis, o que deixou muita gente em dúvida sobre qual deve ser usada.

Mesmo quando havia apenas a função “=QUARTIL”, seu método interno de funcionamento deixava muitas pessoas curiosas sobre o algoritmo que o Excel usa para determinar os quartis. Considere o conjunto de dados a seguir, com 12 valores dispostos em ordem crescente:

Como estamos lidando com 12 valores, fica fácil dividir o conjunto de dados em quatro partes, cada uma com três valores. Mas qual seria os valores exatos do primeiro quartil (Q1), segundo quartil (também chamado de mediana) e do terceiro quartil (Q3)? Pela figura, sabemos que o valor de Q1 deve ser alguma coisa entre 6 e 8, mas falta dizer qual é esse valor. Você poderia dizer que o valor 7 seria um resultado “justo” para Q1, pois fica bem no meio dos valores 6 e 8. No entanto, se você usar a fórmula “=QUARTIL” do Excel, você descobrirá que o primeiro quartil é igual a 7,5. E se você usar a função “=QUARTIL.EXC”, o resultado será 6,5. Como o Excel chega a esses valores? Se você é curioso e gosta de entender como as coisas funcionam, vou explicar até o final deste artigo como funciona cada uma das funções. Isso te ajudará a entender qual delas deve ser usada em cada situação.

Funções Disponíveis no Excel

O primeiro passo é entendermos que não há um método padrão para cálculo de quartis. Nos artigos listados ao final deste post podemos ver que há ao menos 6 métodos diferentes para cálculo de quartis. A seguir são dadas descrições breves das três funções usadas no Excel:

=QUARTIL: Esta função é a única existente para cálculo de quartis no Excel até a versão 2007 e utiliza o método de interpolação linear com base N-1, onde N é a quantidade de elementos no conjunto de dados. Nas versões mais recentes do Excel, esta função continua existindo para fins de compatibilidade com arquivos mais antigos, mas não deve mais ser usada em arquivos novos, pois poderá deixar de existir em versões futuras;

=QUARTIL.INC: Esta função faz exatamente o que a função “=QUARTIL” fazia, utilizando exatamente o mesmo algoritmo de cálculo. A extensão INC refere-se ao fato de a abordagem com base N-1 incluir a mediana no cálculo dos quartis. Se você quer calcular quartis em versões mais recentes do Excel e obter os mesmos resultados das versões mais antigas, esta é a função que deve ser usada;

=QUARTIL.EXC: Um novo algoritmo para cálculo de quartis foi implementada por esta função. Trata-se de um método de interpolação linear com base N+1, que simula a exclusão da mediana na determinação dos quartis. É comumente empregado na detecção de outliers usando a amplitude interquartil como estimativa de variabilidade;

Função QUARTIL.INC

Vamos começar entendendo o funcionamento interno da função QUARTIL.INC, que implementa o mesmo algoritmo da função QUARTIL. Para isso, considere o conjunto de dados apresentado anteriormente. O primeiro passo é colocar os valores em ordem crescente. Em seguida, precisamos rotular cada valor usando números entre 0 e N-1. Em nosso exemplo, isso significa utilizar números entre 0 e 11 para identificar cada valor do conjunto de dados.

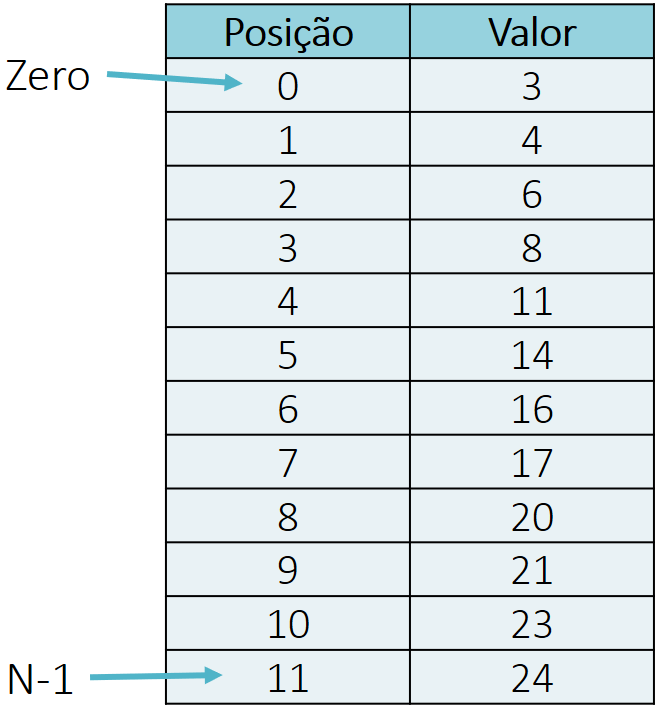
Em seguida, precisamos definir em que pontos ocorrerão os cortes do conjunto de dados. A seguir podemos ver as fórmulas usadas pelo Excel, seguidos dos resultados do exemplo.

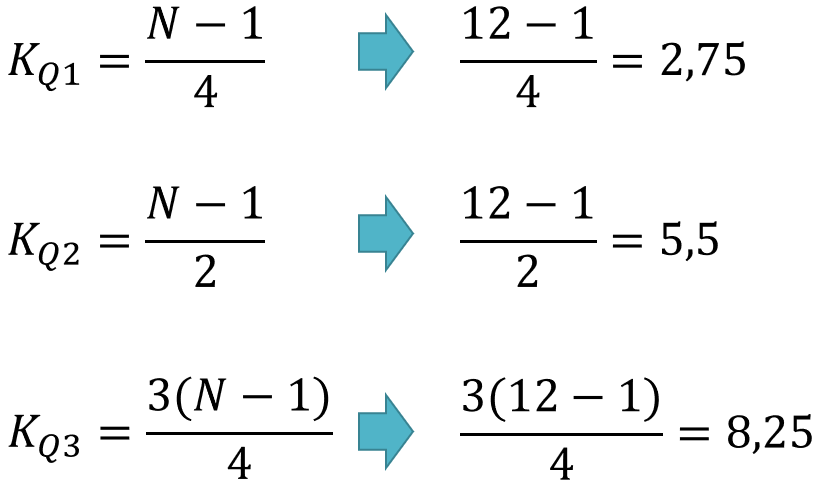
Esses valores não são os quartis ainda, mas sim os pontos em que o conjunto de dados é separado. Por exemplo, o corte do Quartil 1 ocorre na posição 2,75. Isso quer dizer que o Quartil 1 não é nem o valor 6 (que está na posição 2), nem o valor 8 (posição 3), mas sim o valor equivalente à posição 2,75.

Veja na Figura abaixo a representação do Quartil 1. No gráfico temos os valores do conjunto de dados (Eixo Y) plotados em função da sua posição (Eixo X). Podemos ver graficamente que o Quartil 1, na posição 2,75, é equivalente ao valor 7,5 no Eixo Y.

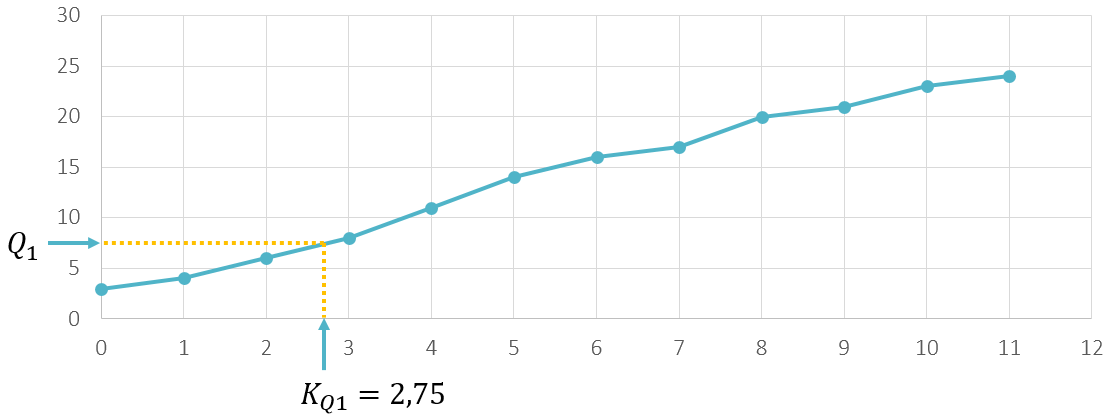
Para entendermos como calcular o valor de Q1, basta pensarmos da seguinte forma: Q1 não é nem o valor 6 (posição 2), nem o valor 8 (posição 3), mas o valor que está em 75% do caminho entre 6 e 8. Isso porque a posição que estamos interessados é a 2,75, que está a 75% do caminho entre 2 e 3. Logo, podemos fazer o seguinte cálculo para obter Q1.

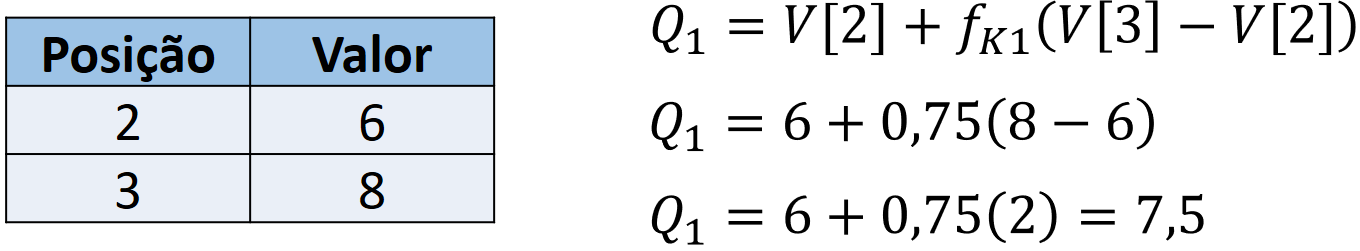
Ou seja, tomamos o valor da posição 2 como base e somamos a ele 75% da diferença entre os valores das posições 3 e 2. Podemos replicar o mesmo para os quartis 2 e 3, cujas posições de corte são 5,5 e 8,25.

Função QUARTIL.EXC

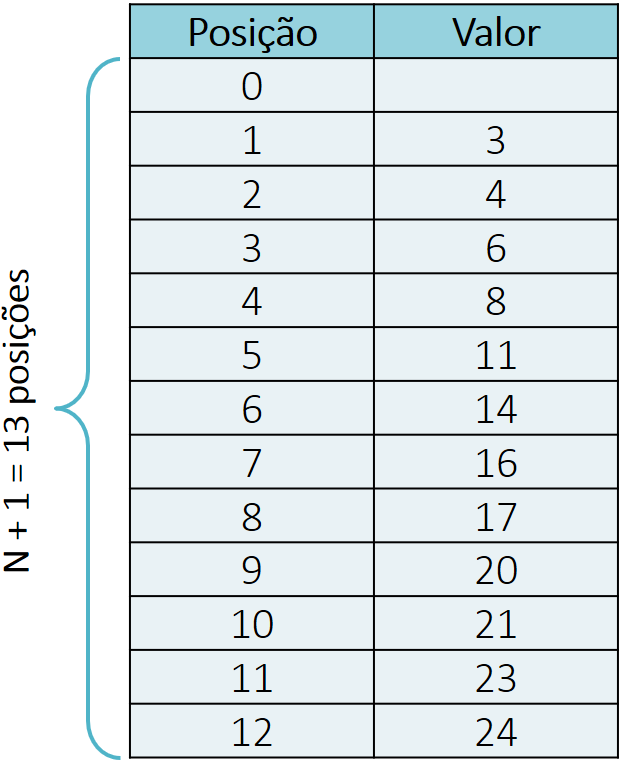
O algoritmo de cálculo da função QUARTIL.EXC é muito similar ao da função QUARTIL.INC. A principal diferença está na numeração dos valores do conjunto de dados. Essa numeração deve ser feita considerando que o identificador 0 vem antes do primeiro valor, estando associado a um espaço vazio do conjunto de dados. O primeiro valor propriamente dito recebe o identificador 1. A numeração resultante terá N+1 rótulos. Em nosso exemplo, teremos a seguinte numeração para a função QUARTIL.EXC:

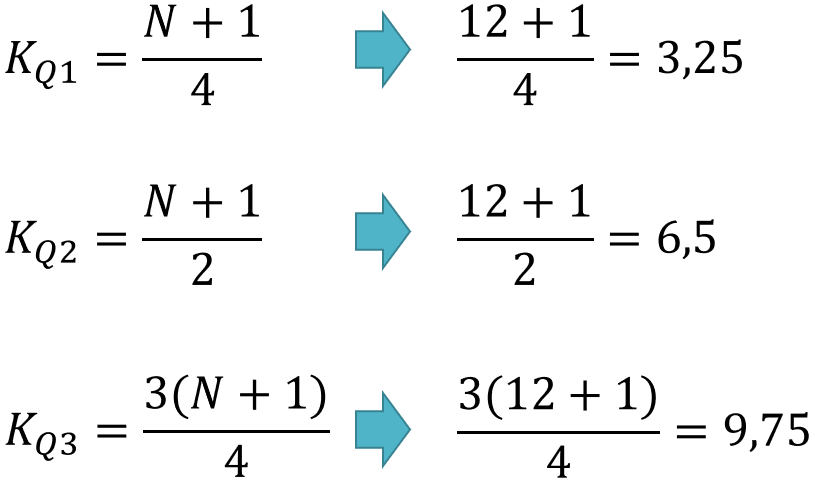
Agora precisamos calcular os pontos de corte. Repare que as fórmulas usam N+1 na parte superior das frações.

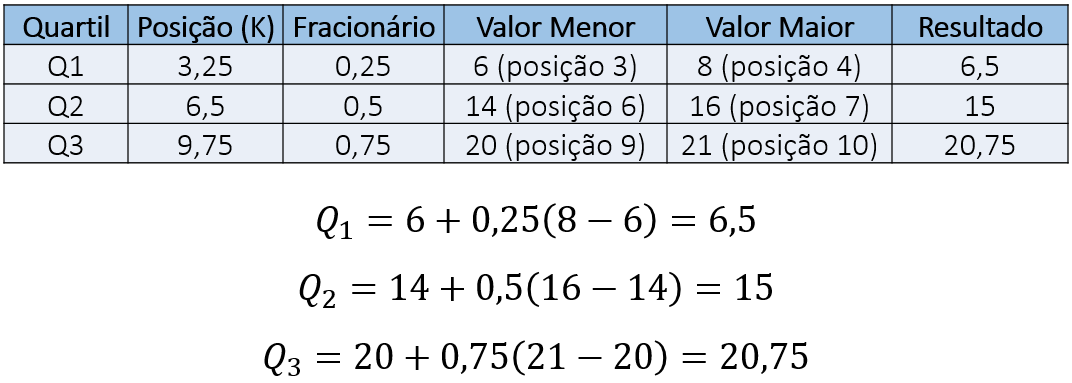
Com base nessas posições de corte, podemos empregar o mesmo método para obter os quartis. A seguir podemos ver os resultados do cálculo dos quartis:

Considerações Finais

Neste artigo vimos que o Excel oferece 2 métodos para cálculo dos quartis. Em geral, não há um método padrão ou que seja melhor que o outro. A principal diferença entre ambos os métodos é que o QUARTIL.EXC sempre oferece uma amplitude interquartil (IQR) maior. Veja na tabela abaixo a amplitude interquartil usando ambas as funções em nosso exemplo.

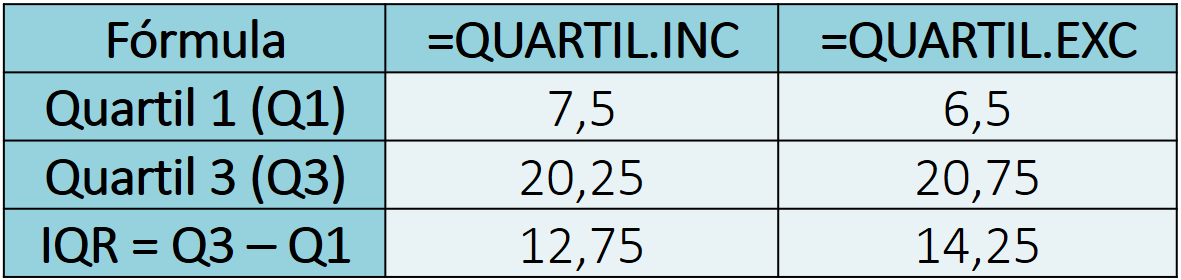
A amplitude interquartil é um importante indicador de variabilidade do conjunto de dados, sendo comumente empregado na identificação de outliers. Por oferecer um resultado maior para o IQR, a função QUARTIL.EXC é mais recomendada quando a finalidade é encontrar outliers. Concluir que um ponto é um outlier mesmo usando um indicador de variabilidade maior nos dá maior segurança quanto a conclusão obtida.

Vale ressaltar que outros softwares estatísticos como o Minitab, SAS, Maple e R oferecem outros algoritmos para cálculo de quartis.